Dynex
Compute on Dynex
Dynex SDK
Customers can run computations on the decentralised Dynex neuromorphic computing platform, which is empowered by a growing number of contributing workers. These are miners who are running the proprietary Proof-of-Useful-Work (PoUW) algorithm DynexSolve. Dynex’s proprietary job management and scheduling system Dynex Mallob ensures that computing jobs are being distributed and computed in the fastest way possible.
Computations are performed by initialising the Dynex processing unit (DPU) into a ground state of a known problem and annealing the system toward the problem to be solved such that it remains in a low energy state throughout the process. At the end of the computation, each state ends up as either a 0 or 1. This final state is the optimal or near-optimal solution to the problem to be solved. In practice, it can be used as an Ising/QUBO sampler.

Dynex SDK
The Dynex SDK provides a neuromorphic Ising/QUBO sampler which can be called from any Python code. Developers and application developers already familiar with the Dimod framework, PyQUBO or the Ocean SDK will find it very easy to run computations on the Dynex neuromorphic computing platform: The Dynex Sampler object can simply replace the default sampler object which typically is used to run computations on, for example, the D-Wave system – without the limitations of quantum machines. The Dynex SDK is a suite of open-source Python tools for solving hard problems with neuromorphic computing which helps reformulate your application’s problem for solution by the Dynex computing platform. It also handles communication between your application code and the Dynex neuromorphic computing platform automatically.
Learn more
Dimod: A shared API for QUBO/Ising samplers
Dimod is a shared API for samplers. It provides classes for quadratic models—such as the binary quadratic model (BQM) class that contains Ising and QUBO models used by samplers such as the Dynex Neuromorphic Platform or the D-Wave system—and higher-order (non-quadratic) models, reference examples of samplers and composed samplers and abstract base classes for constructing new samplers and composed samplers:
PyQubo: QUBOs or Ising models from flexible mathematical expressions
PyQUBO allows you to create QUBOs or Ising models from flexible mathematical expressions easily. It is Python based (C++ backend), fully integrated with Ocean SDK, supports automatic validation of constraints and features placeholder for parameter tuning.
Next Generation Algorithms for Machine Learning
Quantum computing algorithms for machine learning harness the power of quantum mechanics to enhance various aspects of machine learning tasks. As both, quantum computing and neuromorphic computing are sharing similar features, these algorithms can also be computed efficiently on the Dynex platform – but without the limitations of limited qubits, error correction or availability:
Quantum Support Vector Machine (QSVM): QSVM is a quantum-inspired algorithm that aims to classify data using a quantum kernel function. It leverages the concept of quantum superposition and quantum feature mapping to potentially provide computational advantages over classical SVM algorithms in certain scenarios.
> Example Jupyter NotebookQuantum Principal Component Analysis (QPCA): QPCA is a quantum version of the classical Principal Component Analysis (PCA) algorithm. It utilizes quantum linear algebra techniques to extract the principal components from high-dimensional data, potentially enabling more efficient dimensionality reduction in quantum machine learning.
Quantum Neural Networks (QNN): QNNs are quantum counterparts of classical neural networks. They leverage quantum principles, such as quantum superposition and entanglement, to process and manipulate data. QNNs hold the potential to learn complex patterns and perform tasks like classification and regression, benefiting from quantum parallelism.
Quantum K-Means Clustering: Quantum K-means is a quantum-inspired variant of the classical K-means clustering algorithm. It uses quantum algorithms to accelerate the clustering process by exploring multiple solutions simultaneously. Quantum K-means has the potential to speed up clustering tasks for large-scale datasets.
> Example Jupyter NotebookQuantum Boltzmann Machines (QBMs): QBMs are quantum analogues of classical Boltzmann Machines, which are generative models used for unsupervised learning. QBMs employ quantum annealing to sample from a probability distribution and learn patterns and structures in the data.
> Example Jupyter NotebookQuantum Support Vector Regression (QSVR): QSVR extends the concept of QSVM to regression tasks. It uses quantum computing techniques to perform regression analysis, potentially offering advantages in terms of efficiency and accuracy over classical regression algorithms.
Quantum & Neuromorphic Computing Outperform Traditional Methods
A new approach using simulated quantum annealing (SQA) to numerically simulate quantum sampling in a deep Boltzmann machine (DBM) was presented in [1]. The authors proposed a framework for training the network as a quantum Boltzmann machine (QBM) in the presence of a significant transverse field for reinforcement learning. However, they demonstrated that the process of embedding Boltzmann machines in larger quantum annealer architectures is problematic when huge weights and biases are needed to emulate the Boltzmann machine’s logical nodes using chains and clusters of physical qubits. On the other hand, quantum annealing has the potential to speed up the sampling process exponentially.
The Dynex Neuromorphic Platform does not have these physical limitations and can therefore overcome such scaling problems and expand to large, real-world datasets and problems.
Example: Quantum-Boltzmann-Machine (QBM)
This example demonstrates a Quantum-Boltzmann-Machine (QBM) implementation using the Dynex platform to perform the computations and compare it with a traditional Restricted-Boltzmann-Machine (RBM). RBM is a well-known probabilistic unsupervised learning model which is learned by an algorithm called Contrastive Divergence. An important step of this algorithm is called Gibbs sampling – a method that returns random samples from a given probability distribution. We decided to conduct our experiments on the popular MNIST dataset considered a standard benchmark in many of the machine learning and image recognition subfields. The implementation follows a highly optimised QUBO formulation.
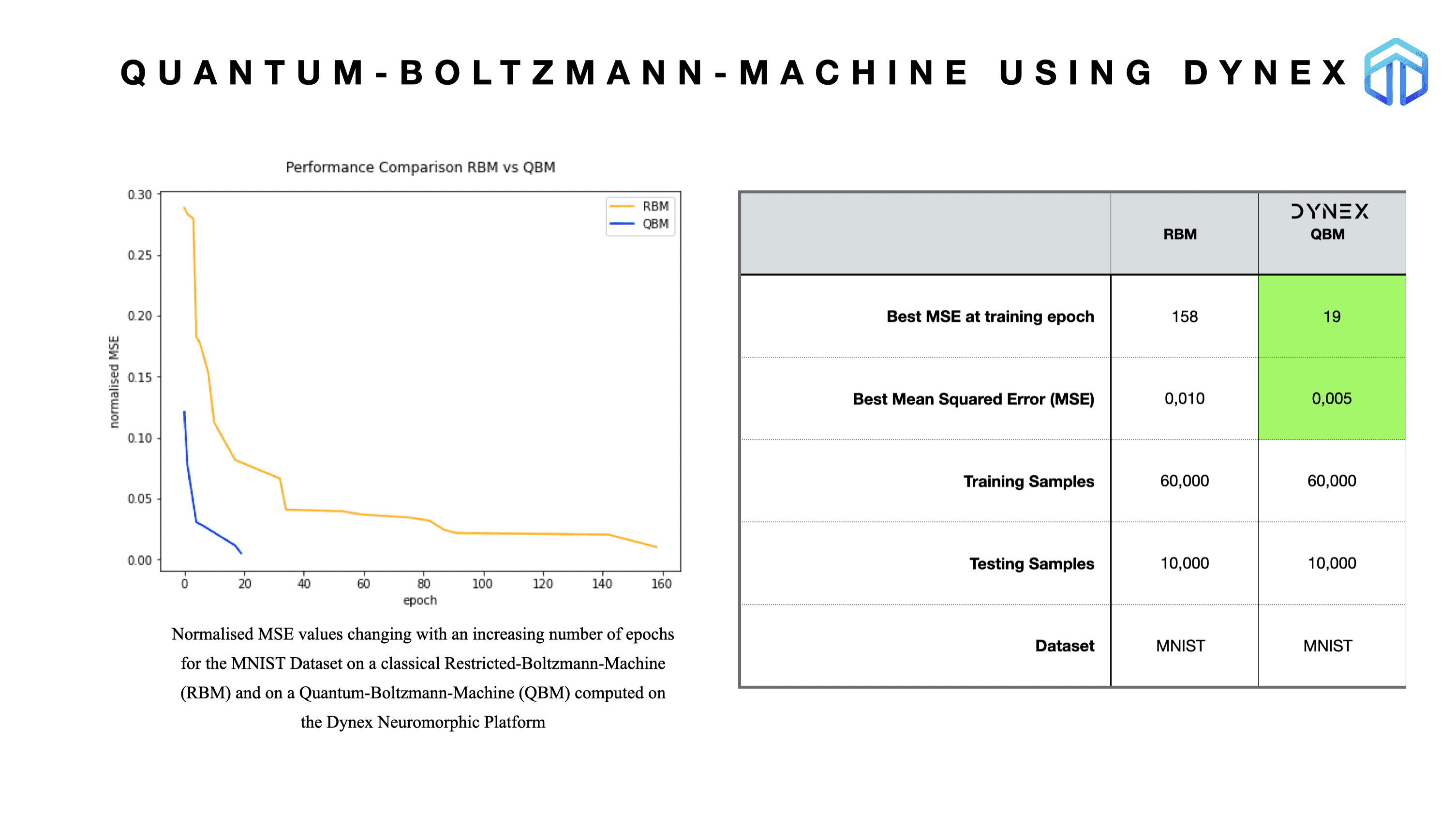
Figure: The QBM evolves much faster to an attractive Mean Squared Error (MSE) than the traditional RBM, which means a significant lower amount of training iterations is required. In addition is the achieved MSE much lower, meaning the QBM created models have higher accuracy. This finding is in line with the results from the papers referenced. However, [1] demonstrated that the process of embedding Boltzmann machines in larger quantum annealer architectures is problematic when huge weights and biases are needed to emulate the Boltzmann machine’s logical nodes using chains and clusters of physical qubits because of the limited number of qubits available. The Dynex Neuromorphic platform provides a more scalable alternative and can used to train models with millions of variables. Especially when real-world models are to be trained, the number of training iterations and accuracy are important.
Example: Quantum-Support-Vector-Machine (QSVM)
In another example, we ran simulations for the Standard Banknote Authentication dataset and measured the following Key Performing Indicators (KPIs) using a Quantum Support Vector Machine (QSVM):
Accuracy: the fraction of samples that have been classified correctly
Precision: proportion of correct positive identifications over all positive identifications
Recall: proportion of correct positive identifications over all actual positives
F1 score: harmonic mean of the model’s precision and recall
Here are the results:

Figure: Quantum (D-Wave) and Neuromorphic (Dynex) based SVM model training is superior to traditional support vector machines. We used Scikit-learn’s LIBSVM using Sequential Minimal Optimisation as benchmark